[Python] 최단 경로 알고리즘 - 다익스트라 알고리즘 (Dijkstra Algorithm)

최단 경로 알고리즘이란 주어진 노드와 간선(edge)들 중, 가장 짧은 경로를 찾는 알고리즘입니다. 즉, 서울에서 인천, 대전, 광주, 부산을 갈 수 있는 가장 짧은 경로를 찾는 것입니다.

최단 경로 문제는 아래와 같이 3가지로 주어질 수 있습니다.

1. 특정 노드에서 시작해 특정 노드까지 도착하는 가장 짧은 경로
2. 특정 노드에서 시작해 모든 노드까지 도착할 수 있는 가장 짧은 경로
   1. 위 예시처럼 서울에서 시작해 서울-인천, 서울-대전, 서울-광주, 서울-부산 간 가장 짧은 거리를 찾는 문제
   2. 여기서 이동 경로가 양수라 하면 Dikjstra 알고리즘이고 음수를 포함한다면 Bellman-ford 알고리즘
3. 모든 노드에서 도착할 수 있는 가장 짧은 경로 (floyd 알고리즘)

여기서 다익스트라 알고리즘은 2번에 해당되는 알고리즘으로 특정 노드에서 시작해 인접한 노드의 가장 짧은 경로들을 탐색하며 모든 노드의 최소 경로를 구하는 알고리즘입니다. 다익스트라 알고리즘은 greedy 알고리즘으로 현재 상황에서 최선의 선택을 진행하며 단방향, 양방향(사이클) 모두 사용할 수 있습니다. 다익스트라는 너비 우선 탐색(BFS) 방식과 유사하며 시작 노드에서 모든 노드 간의 거리 값을 저장하는 배열을 생성한 다음, 인접한 노드들의 거리를 구해 가장 짧은 경로를 해당 배열에 업데이트 해나가는 방식입니다. 다익스트라를 구현하는 방식은 여러가지지만 여기서는 우선 순위 큐를 사용한 방식을 설명합니다.

우선 순위 큐는 최소 힙 방식을 사용해 가장 짧은 경로를 가장 먼저 추출하는 방식을 사용합니다.

예시

아래와 같은 A, B, C, D, E 노드 간 edge가 있고 A에서 출발한다고 가정합니다.

방식

1. 노드간 최소 거리를 저장하는 배열은 시작 노드인 A는 0, 나머지 노드는 무한대(inf)로 설정합니다.
2. 우선 순위 큐(최소 힙)에 시작 노드 A의 거리 (0)을 추가
3. 우선 순위 큐에서 데이터 추출
4. 추출된 노드에서 이동할 수 있는 노드들의 거리와 배열에 저장되어 있는 거리를 비교

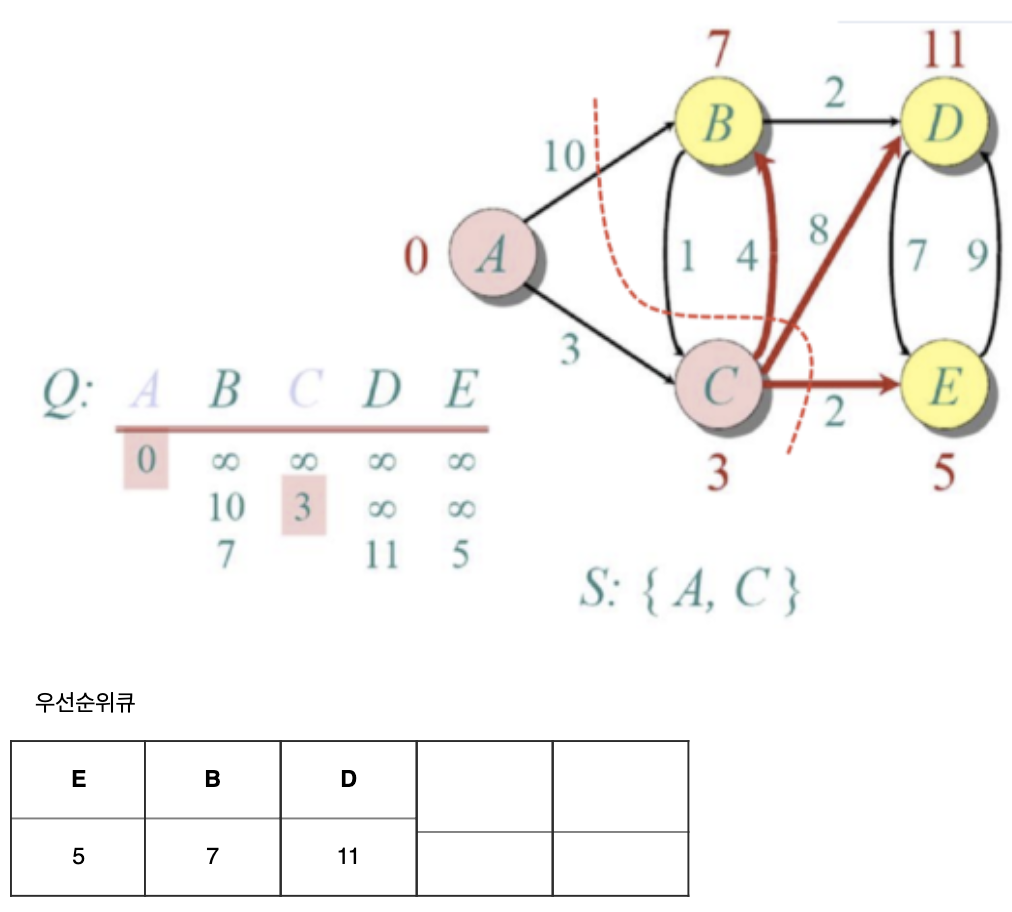
• 맨 처음에는 A 의 거리 (0)이 추출됩니다. 처음 노드 A에서 이동할 수 있는 노드 B와 C의 거리와 배열에 저장되어 있는 거리를 비교

5. 배열 저장된 거리보다 추출된 노드에서 이동할 수 있는 노드의 거리가 더 짧으면 업데이트

• 초기 B와 C에는 무한대 값이 저장되어 있으므로 B는 10, C는 3이 업데이트

6. 배열에 데이터가 업데이트 된 경우, 우선 순위 큐에 삽입

• B와 C가 업데이트 되었으므로 우선 순위 큐에 10과 3을 삽입 - 우선 순위 큐(최소 힙)에 의해 C(3)이 가장 앞으로 정렬

→ 이러한 방식 때문에 너비 우선 탐색(BFS)와 유사하게 첫 노드에서 시작해 인접한 노드들을 방문

7. 3~6번 우선 순위 큐에서 꺼낼 데이터가 없을때까지 반복

설명

시간 복잡도

시간 복잡도는 2가지가 있습니다.

1. 기준 노드에서 인접한 노드를 이동하는 모든 간선
2. 우선 순위 큐에 데이터 삽입/삭제

1번의 경우, 주어진 노드 간의 모든 간선(edge)를 이동하며 검사하므로 간선의 개수만큼의 시간이 소요됩니다. = O(E)

2번의 경우, 데이터에 대한 삽입/삭제가 최악의 경우에 간선의 개수만큼 발생하므로 O(E)이고 삽입/삭제가 발생했을 때, 최소 힙을 유지하는 비용은 O(logE)가 발생합니다 = O(ElogE)

• 힙은 완전 이진 트리로서 재구성 하는데 트리의 높이만큼의 비용이 발생 O(H) = O(logN)

즉, O(E) + O(ElogE) 이므로 총 시간 복잡도는 O(ElogE)입니다.

코드

파이썬에서는 heapq 라이브러리가 있어서 우선 순위 큐를 직접 구현할 필요가 없습니다. heapq에 대해선 https://brownbears.tistory.com/550 에서 자세하게 설명되어 있습니다.

import heapq
import sys

def dijkstra(start):
    # 초기 배열 설정
    distances = {node: sys.maxsize for node in graph}
    # 시작 노드의 거리는 0으로 설정
    distances[start] = 0
    queue = []
    # 시작 노드부터 탐색 시작 하기 위함. (거리, 노드) - 거리, 노드 순으로 넣은 이유는 heapq 모듈에 첫 번째 데이터를 기준으로 정렬을 진행하기 때문 (노드, 거리) 순으로 넣으면 최소 힙이 예상한대로 정렬되지 않음
    heapq.heappush(queue, (distances[start], start))

    # 우선 순위 큐에 데이터가 하나도 없을 때까지 반복
    while queue:
        # 가장 낮은 거리를 가진 노드와 거리를 추출
        current_distance, node = heapq.heappop(queue)
        # 파이썬 heapq에 (거리, 노드) 순으로 넣다 보니까 동일한 노드라도 큐에 저장이 된다 예시: queue[(7, 'B'), (10, 'B')]
        # 이러한 문제를 아래 조건문으로 이미 계산되어 저장한 거리와 추출된 거리와 비교하여 저장된 거리가 더 작다면 비교하지 않고 큐의 다음 데이터로 넘어간다.
        if distances[node] < current_distance:
            continue

        # 대상인 노드에서 인접한 노드와 거리를 순회
        for adjacency_node, distance in graph[node].items():
            # 현재 노드에서 인접한 노드를 지나갈 때까지의 거리를 더함
            weighted_distance = current_distance + distance
            # 배열의 저장된 거리보다 위의 가중치가 더 작으면 해당 노드의 거리 변경
            if weighted_distance < distances[adjacency_node]:
                # 배열에 저장된 거리보다 가중치가 더 작으므로 변경
                distances[adjacency_node] = weighted_distance
                # 다음 인접 거리를 계산 하기 위해 우선 순위 큐에 삽입 (노드가 동일해도 일단 다 저장함)
                heapq.heappush(queue, (weighted_distance, adjacency_node))

    return distances

graph = {
    'A': {'B': 10, 'C': 3},
    'B': {'C': 1, 'D': 2},
    'C': {'B': 4, 'D': 8, 'E': 2},
    'D': {'E': 7},
    'E': {'D': 9},
}

result = dijkstra('A')
print(result)

# {'A': 0, 'B': 7, 'C': 3, 'D': 9, 'E': 5}

위 코드는 시작점에서 모든 노드들의 최소 거리를 구하는 코드입니다. 이를 변형해 특정 노드에서 특정 노드까지의 거리 및 이동 순서를 구할 수 있습니다.