-
[Python] 너비 우선 탐색 (Breadth-First Search, BFS)언어/파이썬 & 장고 2021. 5. 31. 16:43
BFS란?
BFS는 너비 우선 탐색 (Breadth-First Search)로 그래프 탐색 알고리즘 중 하나입니다. 정점에서 같은 레벨에 있는 자식 또는 형제들을 탐색하면서 내려가는 알고리즘입니다. 자세한 내용은 https://brownbears.tistory.com/395 에서 설명이 되어 있습니다.
예제
아래와 같은 그래프가 있다고 가정합니다.
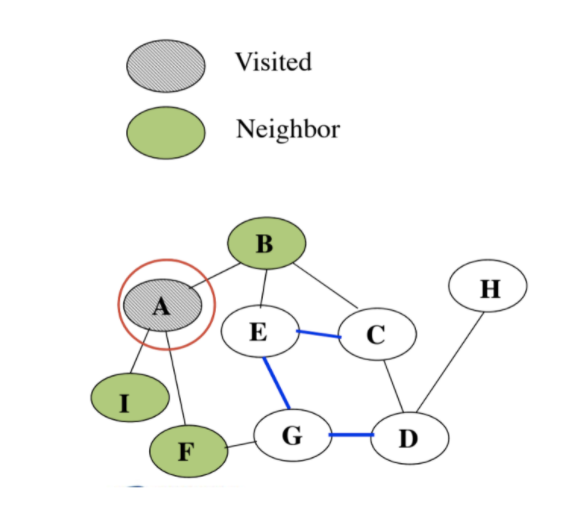
이 그래프를 BFS 알고리즘을 사용하여 모든 노드를 방문한다면 아래와 같은 구조로 탐색을 하게 됩니다.
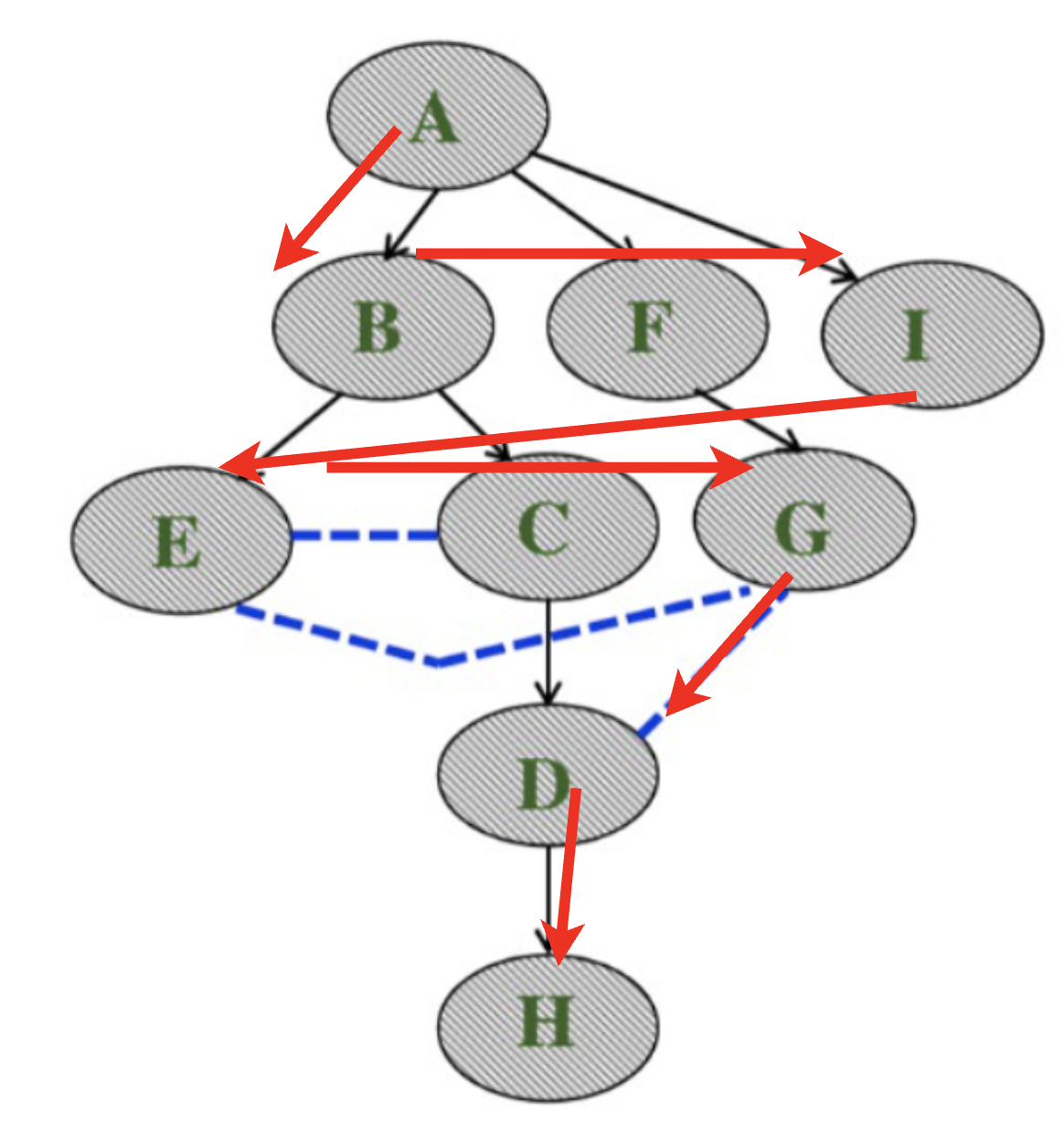
이러한 그래프를 만들기 위해 아래와 같은 형태로 주어졌다고 가정합니다.
graph = { 'A': ['B', 'F', 'I'], 'B': ['A', 'E', 'C'], 'C': ['B', 'E', 'D'], 'D': ['C', 'G', 'H'], 'E': ['B', 'C', 'G'], 'F': ['A', 'G'], 'G': ['E', 'F', 'D'], 'H': ['D'], 'I': ['A'] }BFS는 시작 노드에서 인접한 노드를 방문하고 그 다음, 각 방문한 노드들에서 한 번도 방문하지 않은 인접한 노드를 방문해 나가는 방식입니다. 이를 구현할 때, queue를 사용하면 구현이 간단해집니다.
from collections import deque def bfs(graph, start): visited_nodes = [] adjacency_nodes = deque([start]) while adjacency_nodes: node = adjacency_nodes.popleft() if node not in visited_nodes: visited_nodes.append(node) adjacency_nodes.extend(graph[node]) return visited_nodes graph = { 'A': ['B', 'F', 'I'], 'B': ['A', 'E', 'C'], 'C': ['B', 'E', 'D'], 'D': ['C', 'G', 'H'], 'E': ['B', 'C', 'G'], 'F': ['A', 'G'], 'G': ['E', 'F', 'D'], 'H': ['D'], 'I': ['A'] } bfs(graph, 'A') # ['A', 'B', 'F', 'I', 'E', 'C', 'G', 'D', 'H']BFS의 시간 복잡도는 노드(N) 개수 + 간선(E) 개수로 O(N+E) 입니다.
만약 시작노드로부터 각 노드들의 간선의 가중치를 계산하고자 한다면 아래와 같이 코딩할 수 있습니다.
from collections import deque def bfs(graph, start, distances): adjacency_nodes = deque([start]) visited_nodes = [start] while adjacency_nodes: node = adjacency_nodes.popleft() for adjacency_node in graph[node]: if adjacency_node not in visited_nodes: visited_nodes.append(adjacency_node) adjacency_nodes.append(adjacency_node) distances[adjacency_node] = distances[node] + 1 return visited_nodes, distances graph = { 'A': ['B', 'F', 'I'], 'B': ['A', 'E', 'C'], 'C': ['B', 'E', 'D'], 'D': ['C', 'G', 'H'], 'E': ['B', 'C', 'G'], 'F': ['A', 'G'], 'G': ['E', 'F', 'D'], 'H': ['D'], 'I': ['A'] } distance_dict = dict.fromkeys(graph.keys(), 0) bfs(graph, 'A', distance_dict) # ['A', 'B', 'F', 'I', 'E', 'C', 'G', 'D', 'H'] # {'A': 0, 'B': 1, 'C': 2, 'D': 3, 'E': 2, 'F': 1, 'G': 2, 'H': 4, 'I': 1}