[Python] 최단 경로 알고리즘 - 플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
플로이드 워셜 알고리즘은 다익스트라 알고리즘과 같이 최단 경로를 구하는 알고리즘입니다. 차이점은 다익스트라 알고리즘의 경우, 특정 노드에서 이동할 수 있는 모든 노드에 대해 최소 거리(이 때, 거리(edge)는 양수여야 함)를 구하는 거고 플로이드-워셜 알고리즘은 모든 노드에서 도착할 수 있는 모든 노드의 최소 거리를 구하는 알고리즘입니다. 또한 거리(edge)가 양수 뿐만 아니라 음수여도 사용할 수 있습니다. (다익스트라 알고리즘 설명: https://brownbears.tistory.com/554)
즉, 다익스트라 알고리즘은 서울에서 시작해 인천, 목포, 강릉의 최소 거리를 구하는 것이고 플로이드 워셜 알고리즘은 서울-인천, 서울-목포, 서울-강릉, 인천-목포, 인천-강릉 과 같이 모든 쌍을 한번에 계산합니다.
설명
플로이드 워셜 알고리즘에서는 모든 쌍을 표현하는 이차원 배열을 선언하고 DP (다이나믹 프로그래밍) 기법을 사용하여 각 쌍의 최소 거리를 계산, 업데이트 해나가는 방식입니다.
- 초기에 이차원 배열을 선언할 때, 직접적으로 연결이 되어 있지 않으면 무한대(inf)로 선언하고 자기 자신 (예를 들어, [0,0], [1,1]과 같은 형태)은 0으로 초기화
예를 들어, a → c가 7인데 a → b 는 2, b → c 는 3이라면 a에서 c로 바로 가는 방식이 아닌, a → b → c 와 같이 거쳐서 가는 방식으로 최소 거리 5를 업데이트 합니다.
즉, a → c까지 가는데 걸리는 최단 거리를 구하기 위해선 a → c의 edge와 (a → b의 edge + b → c의 edge) 중 최소값을 업데이트 하는 형식입니다.
플로이드 워셜의 핵심은 a → b → c에서 b와 같이 a에서 c로 가는데 사이에 끼어있는 노드를 기준으로 최단거리를 구하는 것입니다.
예시

그래프는 위와 같고 아래와 같은 형식으로 값이 주어졌다고 가정합니다.
n = 4
data = [[1, 3, -2], [2, 1, 4], [2, 3, 3], [3, 4, 2], [4, 2, -1]]여기서 값을 초기화 하는 방식은 크게 두 가지로 나눠집니다.
1. 자기 자신을 0으로 같이 초기화 하는 방법
dist = []
for i in range(n):
dist.append([])
for j in range(n):
if i == j:
dist[i].append(0)
continue
dist[i].append(sys.maxsize)2. 먼저 inf로 초기화 후, 나중에 자기 자신을 0으로 초기화 하는 방법
dist = [[sys.maxsize] * n for _ in range(n)]
# 나중에 3중 반복문의 첫 번째에서 자기 자신의 값을 0으로 초기화(예시 설명은 2번의 방법으로 진행하겠습니다.)
값의 초기화가 완료되었다면 주어진 값을 위 이차원 행렬에 대입합니다.
for i, j, edge in data:
dist[i - 1][j - 1] = edge- 1을 한 이유는 주어진 값이 1부터 시작하기 때문입니다. 여기까지 완료가 되었다면 아래와 같은 이차원 배열을 가집니다. (K값은 무시)

마지막으로 모든 노드의 가중치를 계산하도록 3중 반복문을 작성합니다.
for k in range(n): # 시작과 종료 사이에 끼어 있는 노드 (중간)
dist[k][k] = 0
for i in range(n): # 시작
for j in range(n): # 종료
dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j]) # 시작 -> 종료와 (시작 -> 중간 + 중간 -> 종료) 중 작은 가중치 저장여기서 핵심은 가장 첫 번째 반복문은 시작과 종료 사이에 끼어 있는 노드를 표현하는 식이여야 합니다. 위에서 설명한 것과 같이 플로이드 워셜 알고리즘에서는 사이에 끼어있는 노드를 기준으로 최단 거리를 구하기 때문입니다. 아래에서 첫 번째 반복문인 k를 기준으로 설명을 진행하겠습니다.
K = 0 일 때, (시작 → 1 → 종료 의 최소거리 계산)
1을 거쳐서 지나가는 모든 노드들의 최소 거리를 계산하는 것입니다.
1을 거쳐가는 케이스는 총 1개이며
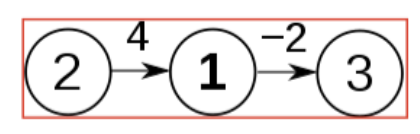
최소값(2 → 3 = 3 , 2 → 1 → 3 = 2) 이므로 dist[2][3]은 2로 대체됩니다.

K = 1 일 때, (시작 → 2 → 종료 의 최소거리 계산)
2을 거쳐서 지나가는 모든 노드들의 최소 거리를 계산하는 것입니다.
2를 거쳐가는 케이스는 총 2개이며
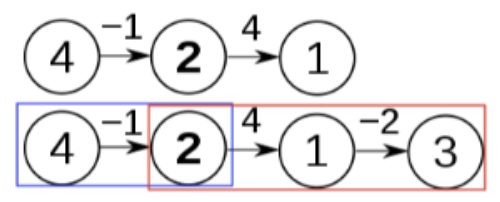
값 K = 0일때와 동일하게 최소값(기존값, 거쳐간 값끼리의 합산)을 진행해 더 작은 값으로 대체합니다.

K = 2 일 때, (시작 → 3 → 종료 의 최소거리 계산)
3을 거쳐서 지나가는 모든 노드들의 최소 거리를 계산하는 것입니다.
3를 거쳐가는 케이스는 총 2개이며
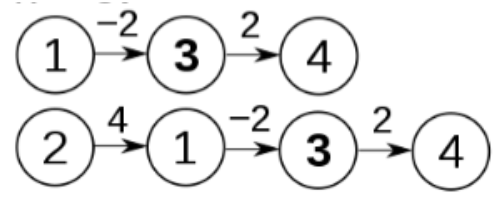
값 K = 0일때와 동일하게 최소값(기존값, 거쳐간 값끼리의 합산)을 진행해 더 작은 값으로 대체합니다.

K = 3 일 때, (시작 → 4 → 종료 의 최소거리 계산)
4를 거쳐서 지나가는 모든 노드들의 최소 거리를 계산하는 것입니다.
4를 거쳐가는 케이스는 총 3개이며

값 K = 0일때와 동일하게 최소값(기존값, 거쳐간 값끼리의 합산)을 진행해 더 작은 값으로 대체합니다.

이와 같이 진행되며 총 코드는 아래와 같습니다.
import sys
def floyd_warshall(n, data):
dist = [[sys.maxsize] * n for _ in range(n)]
for i, j, edge in data:
dist[i - 1][j - 1] = edge
for k in range(n):
dist[k][k] = 0
for i in range(n):
for j in range(n):
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
return dist
n = 4
data = [[1, 3, -2], [2, 1, 4], [2, 3, 3], [3, 4, 2], [4, 2, -1]]
result = floyd_warshall(n, data)
# [[0, -1, -2, 0], [4, 0, 2, 4], [5, 1, 0, 2], [3, -1, 1, 0]]참고 및 이미지 출처
https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm